MRA 453 p.12,13,17 - août 1977 - Gérard Porcher
Cacahuète, Essais et Réflexions.
Trois ans que les cacahuètes sont montées à Paris et pourtant déjà le manque de gymnases se fait sentir.
Quand et comment les sportifs attitrés comprendront-ils notre besoin d'utiliser une salle au moins deux heures par mois ?
Notre sport favori : l'aéromodélisme, ne s'arrête pas au collage de petits bouts de bois, il comporte une grande partie de son activité en plein air. Tous les modélistes savent cela, particulièrement ceux qui pratiquent le vol libre, je dirais le vol non radiocommandé, car courir après un modèle représente un effort physique non négligeable, souvent en tout terrain, au petit trot ou en jogging, oui c'est du sport !
Et les cacahuètes ? petites maquettes de 33 cm de longueur d'aile ? et bien ce sont avec ces petits modèles que nos jeunes apprennent le plus rapidement à bien construire et bien faire voler! D'un poids moyen de 15 gr elles ne présentent aucun danger et le moteur élastique, silencieux, est propre, mais elles n'aiment pas le vent. C'est pour cela qu'elles doivent voler en intérieur.
L'entraînement à l'abri des intempéries, c'est la préparation aux sorties de plein air, c'est la préparation à notre sport pour modèles de grand air.

L'auteur et son Delanne C20 à l'échelle cacahuète (Peanut Scale)
Technique et cacahuète
La petite taille de ces modèles se prête admirablement à une multitude d'essais, tant sur les profils d'ailes aux petites vitesses que sur les hélices et moteurs caoutchouc. Je pense aussi qu'elles peuvent contribuer à l'étude de modèles plus grands du genre coupe d'hiver ou Wakefield, ce sont donc des maquettes au sens propre du mot.
Tout cela pose des problèmes et la curiosité aidant nous sommes vite dirigés vers la puissance utile, l'énergie restituée des hélices sans oublier pour autant les qualités de vol de la cellule,
Comparaison de modèles
C'est le DELANNE C20 qui fait les frais de l'opération. Ce modèle est très lourd 7.75 gr au dm2. L'hélice de 160 mm au pas de 1.28 semble adpatée mais il faut 8 mm2 de section pour le caoutchouc et 1125 tours d'enroulement pour ne voler que 34 secondes. Au banc, même moteur et même hélice déroulent en 50 secondes. La charge alaire coûte cher puisqu'il n'utilise que 66 % de la durée de déroulement.
Méritte avec son FARMAN 451 déroule 1200 tours en 49 secondes de vol et 50 secondes au banc soit presque 100% d'énergie restituée, 3,2 mm2 de section, hélice de 120. Tout est bien adapté.
Charge alaire 4,3 gr/dm2 + caoutchouc + hélice + qualité de réalisation.
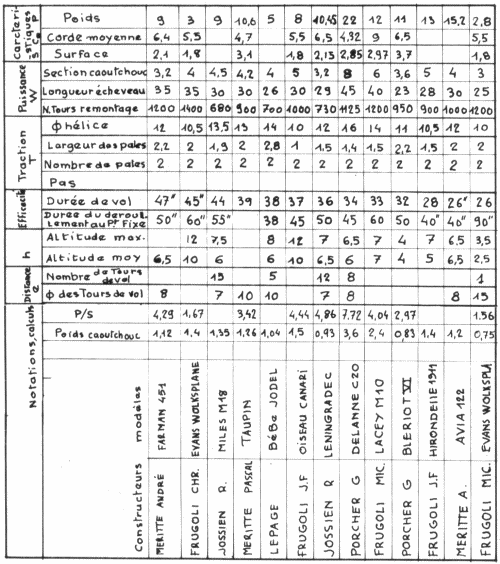
Comparatif des motorisations des cacahuètes
L'Oiseau CANARI de Jean-François Frugoli (4,5 gr au dm2) 6 mm2 de section caoutchouc, vole 37 secondes, déroule au point fixe 45 secondes, 80 % de son énergie est utilisée mais son hélice n'a que 10 cm de diamètre.
Le LENINGRADEC de René Jossien, 6 gr au dm2 utilise 80 % de son énergie et vole 45 secondes avec 5,4 mm2 de section pour une hélice de 120 de diamètre mais fuselage court seulement 730 tours d'enroulement.
Durée de vol
Elle est conditionnée directement par le temps de déroulement du moteur caoutchouc cela paraît évident, mais en fait, c'est la hauteur sous plafond, généraleement de 6 à 7 mètres qui oblige à limiter l'altitude atteinte, plusieurs solutions se présentent.
1) diminuer le nombre de tours, ce qui évidemment diminue le temps de vol.
2) changer l'hélice pour un pas différent semble jouer très peu sur la durée de vol.
3) diminuer la section du caoutchouc abaisse la charge alaire, entraîne une augmentation relative du nombre de tours mais l'écheveau se comporte très mal et fait des queues de cochon.
La tête entre les mains, chevelure hirsute, je me replonge dans les articles de Marcel Chabonat, René Bahout, Jacques Morisset, avec grand profit... et c'est là que la montagne accouche de sa petite souris.
La charge alaire ou Poids du modèle/ Surface de l'aile P/S, détermine la puissance nécessaire du vol, ici la section du caoutchouc.
L'hélice, intermédiaire entre puissance développée et altitude atteinte, doit fournir le maximum de traction pour le minimum d'énergie emportée.
La section du caoutchouc fournit les tours/secondes à l'hélice qui transforme ces tours/seconde en vitesse, cette vitesse donne la portance qui elle, est diminuée par la charge alaire. La vitesse se trouve aussi diminuée par la traînée générale du modèle. C'est donc à ce petit transformateur d'énergie qu'est l'hélice que l'on demande le plus, il faut qu'elle soit adaptée à la vitesse de vol du modèle, à son plafond maximum, qu'elle régule un moteur caoutchouc nerveux et inconstant et c'est seulement à ces conditions qu'elle-même a sa plus grande efficacité.
- Déroulement constant = efficacité de l'hélice
- Maximum de tours/seconde pour minimum de poids de caoutchouc
- Minimum de P/S et minimum de traînée générale pour minimum d'énergie embarquée
Cacahuètes : drôles de petites choses à gros problèmes
Essais au banc (figure 1) : c'est le moteur caoutchouc du Delanne, freiné par son hélice de 16 cm au pas de 1,28 qui nous donne les premières courbes, 1125 tours maxi., les couples (Cm) sont relevés en cours de déroulement. Les tours au déroulement sont décomptés après un stop au temps voulu.
Au temps de déroulement zéro (1125 tours) vitesse de rotation nulle, l'hélice n'est pas lâchée, le couple maxi. est à 600 gr mm.
Au temps :
1" la vitesse de rotation passe de zéro à 37 T/s
3,7" la vitesse de rotation tombe à 22 T/s
6,25" la vitesse de rotation remonte à 36 T/s
10" la vitesse de rotation retombe à 20 T/s
17,5" la vitesse de rotation remonte à 23 T/s
On remarque sur la courbe des vitesses de rotation une oscillation au cours du temps de déroulement, qui s'atténue pour donner presque une droite en fin de déroulement.
Ces oscillations sont dues en grande partie à l'inertie de l'hélice en cours d'accélération. De cette énergie acquise, lorsqu'elle est arrivée au maximum de sa vitesse de rotation, elle en réinjecte une partie en redonnant des tours au moteur caoutchouc mais en en perdant elle-même. Ensuite elle repart pour une nouvelle accélération ces oscillations s'atténuent au cours du temps pour devenir nulles évidemment lorsque ce couple moteur devient nul.
Ce processus d'oscillation est d'autant plus nuisible que l'hélice est lourde donc d'une énergie cinétique importante et que le moteur est puissant.
Dans ce type d'équipage si l'on excepte les 10 premières secondes, les nombres de tours/seconde vont toujours en décroissant, ce qui est généralement admis et souhaitable dans certains cas pour le vol libre, mais en salle, il faut un déroulement constant dans la plus grande partie du vol et une adaptation précise du pas de l'hélice.
- un inconvénient majeur, on voit souvent des modèles de vol libre faire une perte de vitesse, après le départ dans les 3 à 4 secondes : cela correspond au creux de la vague sur notre graphique,
- un autre inconvénient que certains modèles n'acceptent pas le virage à droite, cela est dû à l'effet gyroscopique de l'hélice lourde.
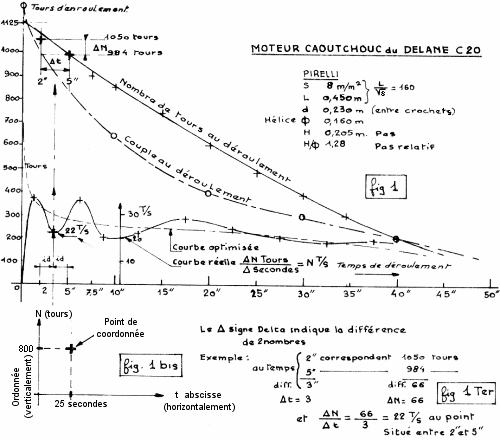
Fig. 1 - Les essais du moteur du Delanne à l'échelle cacahuète (Peanut Scale)
Contrôle des vitesses de rotation (N en tours/seconde)
Matériel nécessaire : du papier, un crayon, une chignole, un chrono.
- Dans l'étau, une grosse baguette en sapin 20 X 20 mm munie d'un crochet et d'un faux couple - avant, avec son nez porte-hélice, ou tout simplement un fuselage réformé mais solide.
- Beaucoup de temps à perdre pour les sceptiques ou les consommateurs de produits finis.
mais aussi
- Technique du modéliste, enrichie par une meilleure connaissance sur la mécanique de vol d'une merveilleuse petite machine de bois et de papier collés.
Essais - Moteur lubrifié et rôdé
Remonter autant de fois au même nombre de tours que l'on veut de points de contrôle.
- 1125 tours, lâcher l'hélice et stop arrêt rapide le doigt dans l'hélice au temps voulu ; compter le nombre de tours qu'il reste.
Voir la figure 1 bis, sur graphique, les tours décomptés sont portés verticalement (ordonnées) et correspondent au temps écoulé horizontalement (abscisses).
Joindre tous les points donne la courbe du nombre de tours au déroulement (fig.1). Son allure générale, optimisée (elle ne passe pas exactement par tous les points) nous indique que le déroulement est presque constant ; si c'était une droite véritable, du point 1125, temps zéro au point 50", la valeur :
nb. de tours maxi / le temps maxi = 1125 / 50
serait de 22,5 T/s. Et la courbe réelle des tours/sec. (Fig. 1) serait une ligne horizontale, donc N tours/ secondes constants d'un bout à l'autre du déroulement. Il en est tout autre.
Calcul des N tours/secondes suivez le guide, fig. 1ter. (à suivre)